In 2010 I co-authored a paper that investigated the locational efficiency of agro-dealers in central Malawi. We analysed the accessibility to existing trained agro-dealers in a raster environment using the ‘costdistance’ algorithm in the ESRI Arc/INFO software. The trained agro-dealers did not cover sufficient population when we modelled farmers’ accessibility using bicycles or walking.
To choose new agro-dealers for training I programmed a ‘greedy-add’ heuristic in Arc Macro Language (AML), accessing points from shapefiles of potential new agro-dealers, and raster grids in native ESRI format.
Since Arc/INFO is no longer a component of ArcGIS I have been investigating how to replicate the heuristic and the accessibility analysis in PostgreSQL/PostGIS and R environments.
I tried two methods, the first used the gdistance and raster packages in R, and the second used the pgRouting and PostGIS extensions in PostgreSQL.
gdistance and raster packages in R
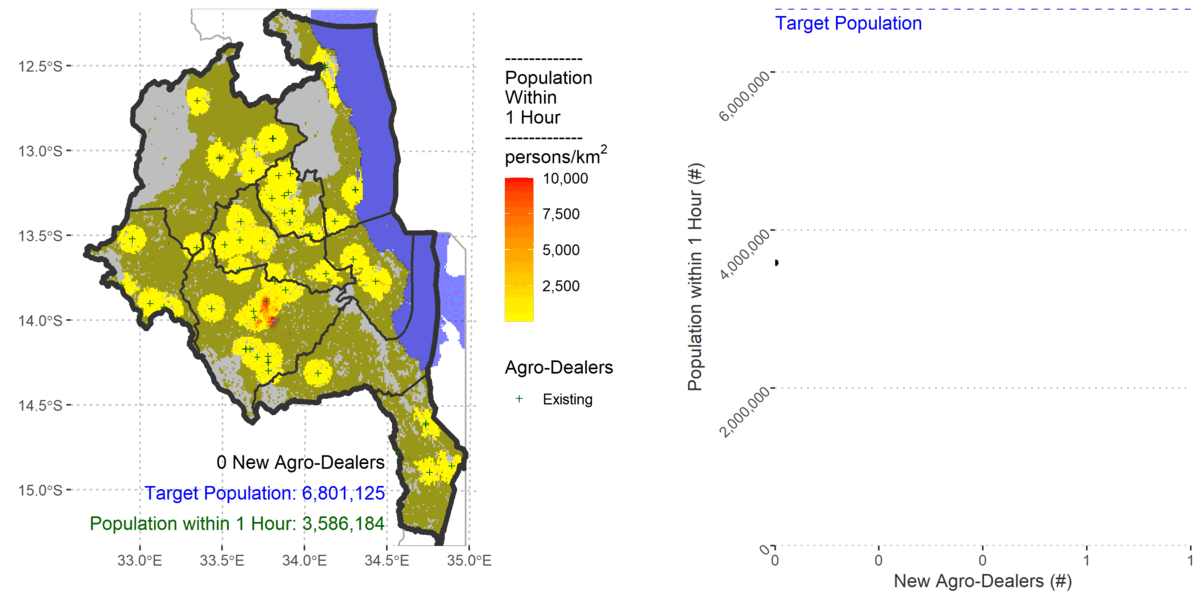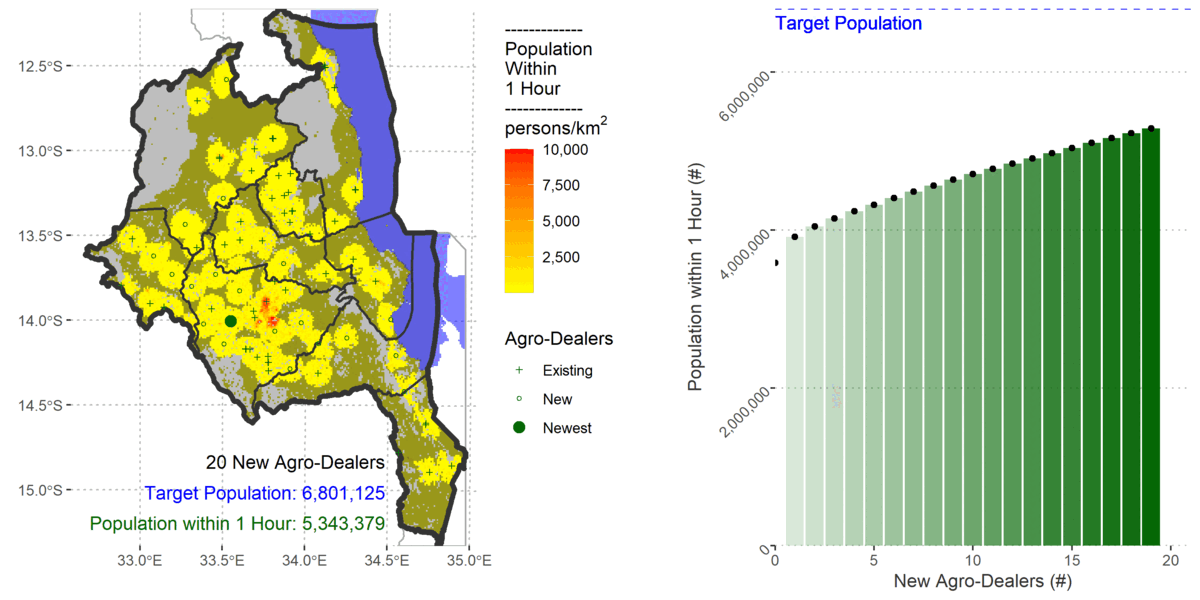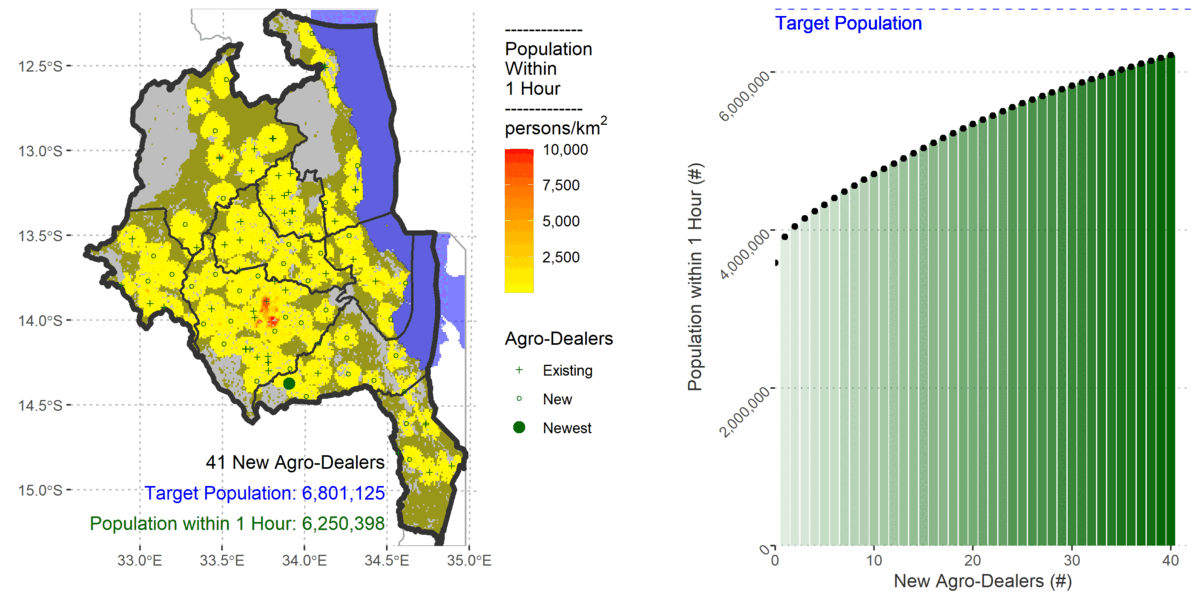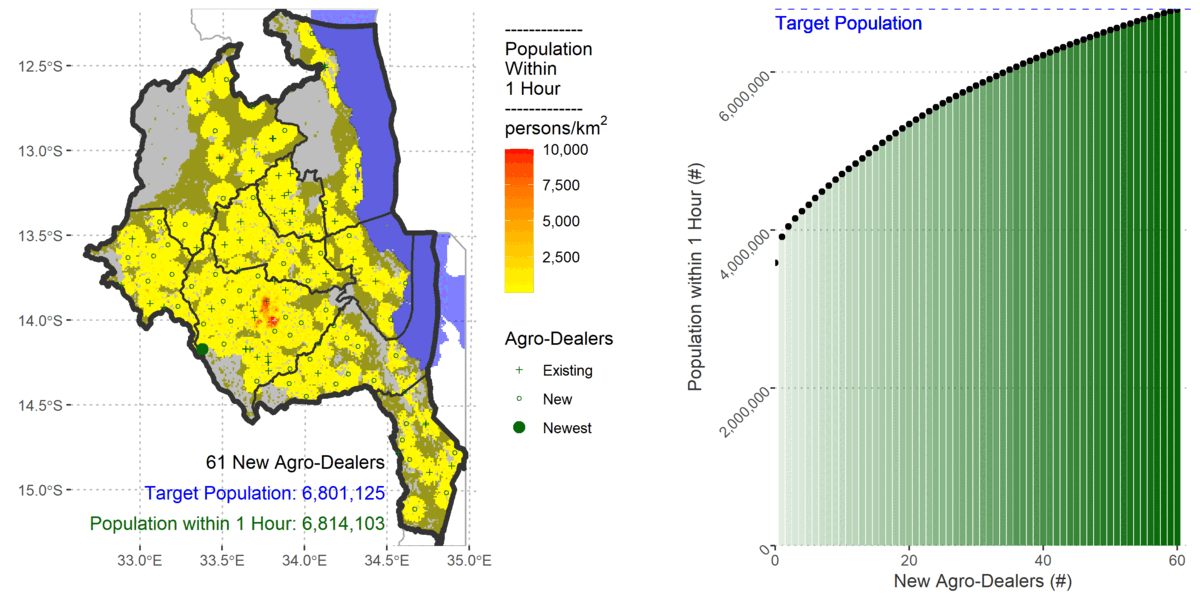
My previous AML approach used existing raster accessibility algorithms within a custom made heuristic for determining near optimal locations of stockists. I followed the same logic in R with only slight differences because gdistance uses a transition layer.
I also updated the population using the 2020 constrained 1km population count from WorldPop, Land Cover from Copernicus, and the road network from OpenStreetMap.
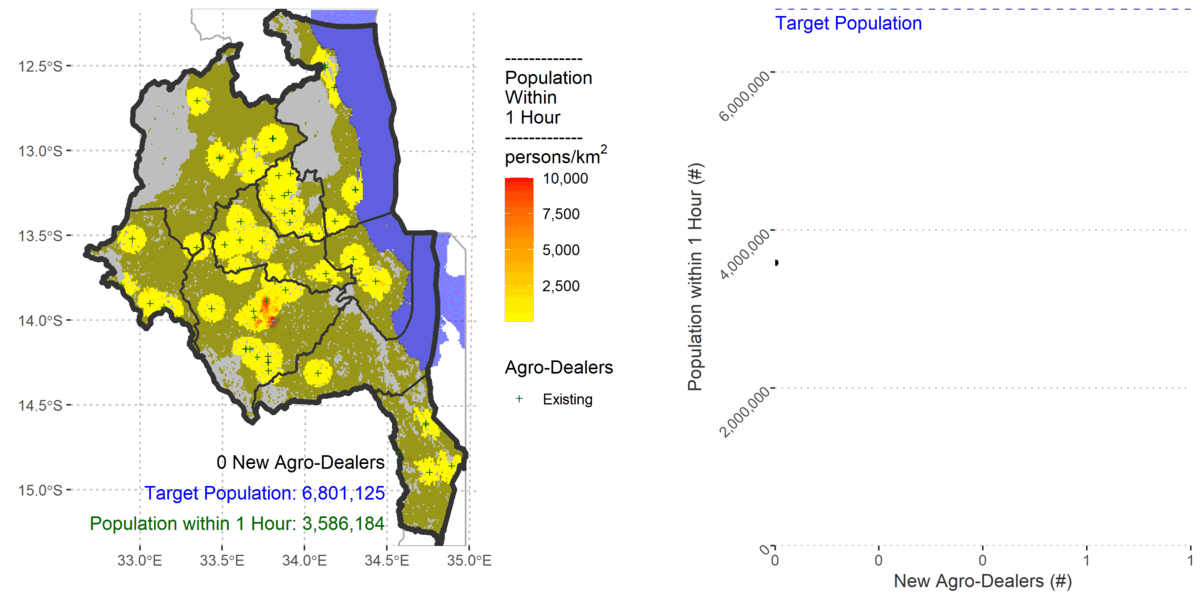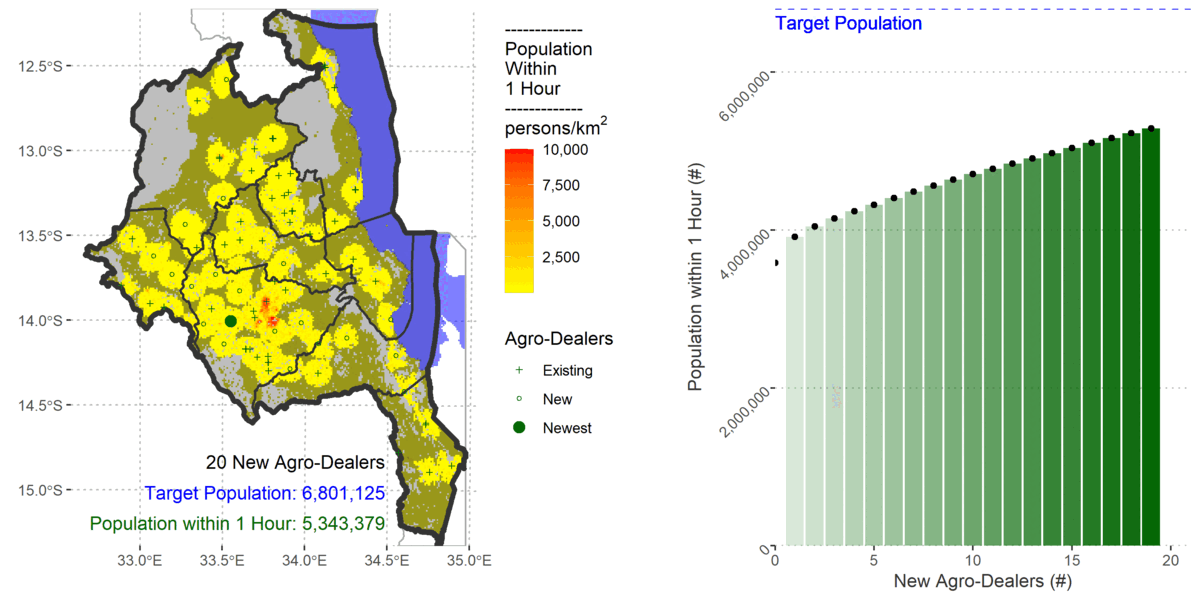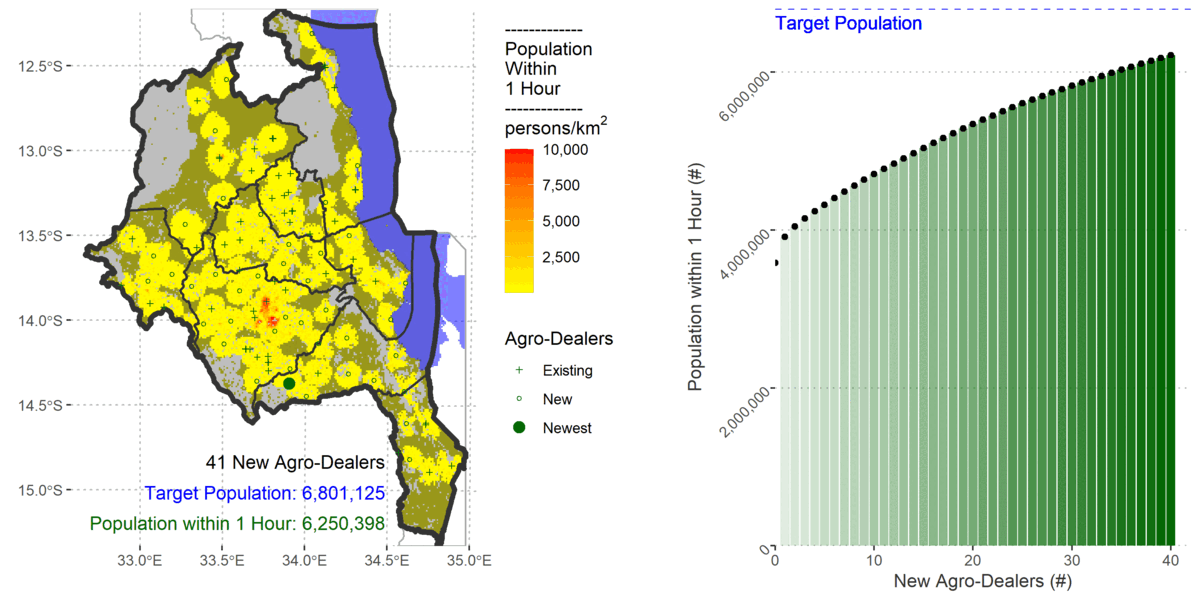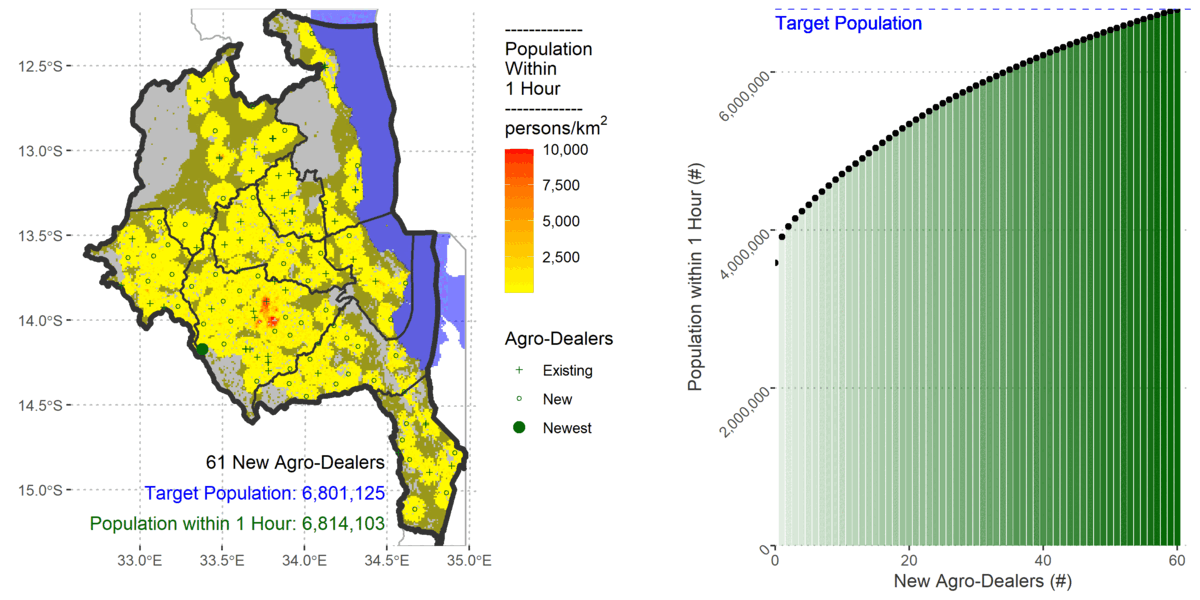
To cover 80% of the population the algorithm added 61 new agro-dealers.
pgRouting and PostGIS extensions in PostgreSQL
The pgRouting library extends the PostGIS / PostgreSQL geospatial database to provide geospatial routing functionality.
The pgRouting library computes the shortest paths in a network of lines (edges) and points (nodes). Consequently, I had to convert my raster friction surfaces to a network of edges – each with a travel time cost.
I also needed to ensure that the nodes on the network had population attributes and that the potential agro-dealer locations were ‘snapped’ to the nodes. I prepared these data using PL/pgSQL scripts, taking advantage of PostGIS spatial indexes.
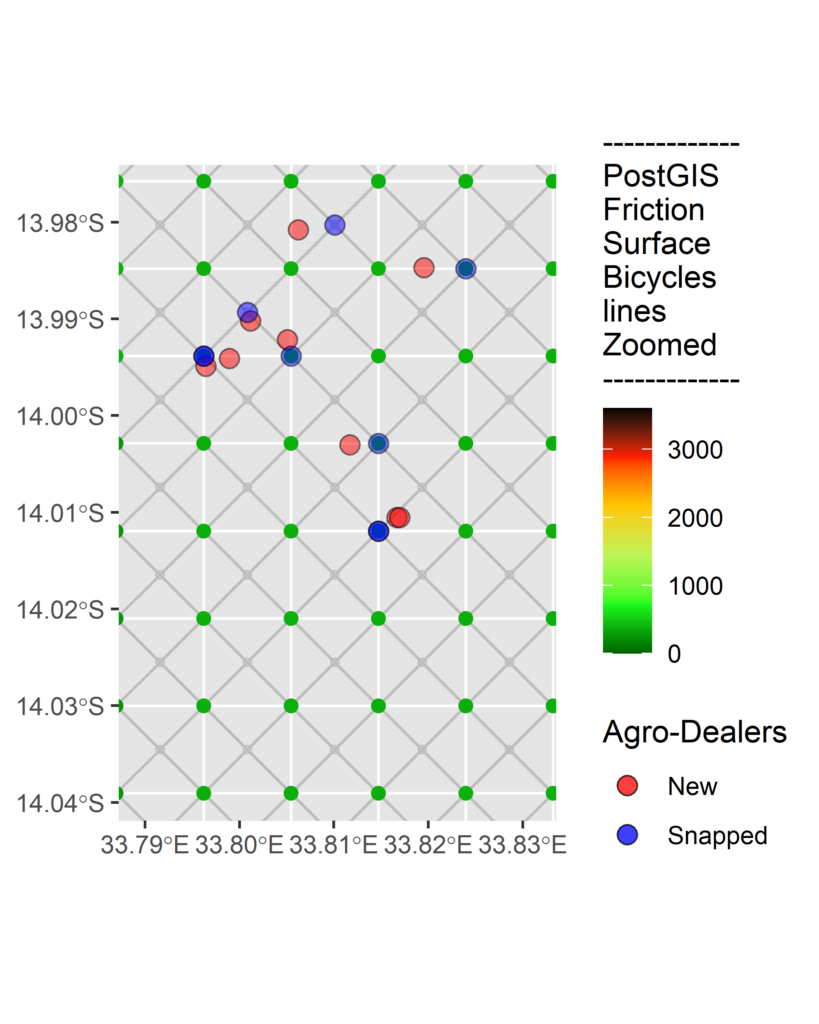
I followed a similar logic to the greedy-add algorithm in R, but using instead the pgrdijkstra function repeatedly over the network and calculating the population of all end-nodes within 1 hour of each potential agro-dealer.
Despite pgrdijkstra and gdistance both using Dijkstra’s shortest path algorithm the vector method in pgRouting only required a further 59 agro-dealers to cover 80% of the population within an hour.
Conclusion
The gdistance method was considerably faster than the pgRouting method, and required less data preparation. Nevertheless, both methods took at least 2 hours to run on an average laptop.
I have yet to discover the reason for the difference in the results of the two algorithms, both consider 8 directions, and I have yet to find differences in the shortest paths between specific sources and targets.
Apart from discovering the discrepancies between the results, my next objective is to see how best to scale these methods and see if it is possible to simplify and potentially automate them.